排序

常见排序算法

记录一些常见的不常见的、沙雕的算法和思想。使用 js 实现。

冒泡排序

• 最常见的排序之一。

// 从小到大排序
function bubbleSort(arr) {
  if (!arr || arr.length < 2) return arr;
  for (let i = arr.length - 1; i > 0; i--) {
    for (let j = 0; j < i; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

快速排序

原理：找到一个基数，把数组分成左右两部分，分别与这个基数比较大小，然后按需要的顺序交换元素的位置，重复上述步骤；

• 有原地排序和非原地排序的区别

1. 原地排序

// min -> max
function devide(arr, start, end) {
  let baseIndex = Math.floor(start + (end - start) / 2),
    i = start,
    j = end;
  let base = arr[baseIndex];
  while (i < j) {
    // 找到左侧比base大的
    while (arr[i] < base) {
      i++;
    }
    // 找到右侧比base小的
    while (arr[j] > base) {
      j--;
    }
    // 交换此时的arr[i]和arr[j]
    if (i <= j) {
      [arr[i], arr[j]] = [arr[j], arr[i]];
      i++;
      j--;
    }
  }
  return i; // 此时arr[i]的位置就在它最终应该在的位置上
}

function quickSort(arr) {
  if (arr.length <= 1) return arr;
  const start = 0;
  const end = arr.length - 1;
  const index = devide(arr, start, end);
  if (start < index - 1) {
    quickSort(arr, start, index - 1);
  }
  if (end > index) {
    quickSort(arr, index, end);
  }
  return arr;
}

2. es6

function quickSort(arr) {
  if (!arr.length) return [];
  const [pivot, ...rest] = arr;
  return [...quickSort(rest.filter((item) => item < pivot)), pivot, ...quickSort(rest.filter((item) => item >= pivot))];
}

插入排序

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    const element = arr[i];
    let j = i - 1;
    for (j; j >= 0; j--) {
      const tmp = arr[j];
      const order = tmp - element;
      if (order > 0) {
        arr[j + 1] = tmp;
      } else {
        break;
      }
    }
    arr[j + 1] = element;
  }
  return arr;
}
// better
function insertionSort(arr) {
  if (!arr || arr.length < 2) return arr;
  for (let i = 1; i < arr.length; i++) {
    for (let j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
      [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
    }
  }
  return arr;
}

选择排序

// 从小到大排序
function selectionSort(arr) {
  if (!arr || arr.length < 2) return arr;
  for (let i = 0; i < arr.length - 1; i++) {
    let minIndex = i; // 当前下标之前的都是有序的了，假设当前下标的值是未排序的数字里面最小的
    for (let j = i + 1; j < arr.length; j++) {
      // 从i~n-1上找最小值下标，然后和minIndex交换
      minIndex = arr[j] < arr[minIndex] ? j : minIndex;
    }
    [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
  }
  return arr;
}

归并排序

• 找到中点，把两边都排好序，然后用两个指针指向两边有序的头部，开始比较并合并

function mergeSort(arr) {
  // 基础情况：如果数组的长度小于或等于1，则返回该数组
  if (arr.length <= 1) {
    return arr;
  }

  // 找到中间索引
  const mid = Math.floor(arr.length / 2);

  // 分别对左半部分和右半部分进行归并排序
  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));

  // 合并已排序的两部分
  return merge(left, right);
}

function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  // 合并两个已排序的数组
  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // 将剩余的元素添加到结果数组中
  return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}

// 示例用法
const array = [38, 27, 43, 3, 9, 82, 10];
const sortedArray = mergeSort(array);
console.log(sortedArray); // 输出：[3, 9, 10, 27, 38, 43, 82]

堆排序

掌握堆的构建方法，然后根据堆的特性进行排序。常用于解决数组排序、TopK 等问题。

function heapSort(arr) {
  const n = arr.length;

  // 构建最大堆
  for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
    heapify(arr, n, i);
  }

  // 一个个取出元素，交换堆顶和最后一个元素，并重新调整堆
  for (let i = n - 1; i > 0; i--) {
    // 交换
    [arr[0], arr[i]] = [arr[i], arr[0]];

    // 重新调整堆
    heapify(arr, i, 0);
  }

  return arr;
}

// 从一个节点开始调整堆
function heapify(arr, n, i) {
  let largest = i; // 初始化最大值为根节点
  const left = 2 * i + 1; // 左子树
  const right = 2 * i + 2; // 右子树

  // 如果左子树比根节点大
  if (left < n && arr[left] > arr[largest]) {
    largest = left;
  }

  // 如果右子树比当前最大的节点还大
  if (right < n && arr[right] > arr[largest]) {
    largest = right;
  }

  // 如果最大节点不是根节点
  if (largest !== i) {
    // 交换
    [arr[i], arr[largest]] = [arr[largest], arr[i]];

    // 递归调整受到影响的子树
    heapify(arr, n, largest);
  }
}

// 示例用法
const array = [38, 27, 43, 3, 9, 82, 10];
const sortedArray = heapSort(array);
console.log(sortedArray); // 输出：[3, 9, 10, 27, 38, 43, 82]

希尔排序

function shellSort(arr) {
  const n = arr.length;
  let gap = Math.floor(n / 2); // 初始增量

  // 逐步减少增量
  while (gap > 0) {
    // 对每个增量进行插入排序
    for (let i = gap; i < n; i++) {
      const temp = arr[i];
      let j = i;

      // 将当前元素插入到对应的有序子数组中
      while (j >= gap && arr[j - gap] > temp) {
        arr[j] = arr[j - gap];
        j -= gap;
      }
      arr[j] = temp; // 插入当前元素
    }
    gap = Math.floor(gap / 2); // 更新增量
  }

  return arr;
}

// 示例用法
const array = [38, 27, 43, 3, 9, 82, 10];
const sortedArray = shellSort(array);
console.log(sortedArray); // 输出：[3, 9, 10, 27, 38, 43, 82]

计数排序

用一个能容纳所有元素的数组（max-min+1），根据下标的相对大小（cur-min）来记录每个值出现的次数，最后遍历这个数组生成所需的结果。

function countingSort(arr) {
  const n = arr.length;
  if (n === 0) return arr; // 如果数组为空，直接返回

  // 找到数组中的最大值和最小值
  const maxVal = Math.max(...arr);
  const minVal = Math.min(...arr);
  const range = maxVal - minVal + 1; // 计算范围大小

  // 创建计数数组并初始化为0
  const count = new Array(range).fill(0);

  // 计数每个元素的出现次数
  for (let i = 0; i < n; i++) {
    count[arr[i] - minVal]++;
  }

  // 将计数数组转换为排序后的数组
  let index = 0;
  for (let i = 0; i < range; i++) {
    while (count[i] > 0) {
      arr[index++] = i + minVal; // 将元素放回原数组
      count[i]--;
    }
  }

  return arr;
}

// 示例用法
const array = [4, 2, 2, 8, 3, 3, 1];
const sortedArray = countingSort(array);
console.log(sortedArray); // 输出：[1, 2, 2, 3, 3, 4, 8]

桶排序

function bucketSort(arr, bucketSize = 5) {
  if (arr.length === 0) return arr; // 如果数组为空，直接返回

  const minVal = Math.min(...arr);
  const maxVal = Math.max(...arr);
  const bucketCount = Math.floor((maxVal - minVal) / bucketSize) + 1;

  // 创建桶
  const buckets = Array.from({ length: bucketCount }, () => []);

  // 将元素放入对应的桶中
  for (let num of arr) {
    const bucketIndex = Math.floor((num - minVal) / bucketSize);
    buckets[bucketIndex].push(num);
  }

  // 对每个桶进行排序
  const sortedArray = [];
  for (let bucket of buckets) {
    // 使用内置的排序方法（例如，快速排序）对每个桶进行排序
    sortedArray.push(...bucket.sort((a, b) => a - b));
  }

  return sortedArray;
}

// 示例用法
const array = [0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.82];
const sortedArray = bucketSort(array);
console.log(sortedArray); // 输出：[0.17, 0.21, 0.26, 0.39, 0.72, 0.78, 0.82, 0.94]

基数排序

function getDigit(num, place) {
  return Math.floor(Math.abs(num) / Math.pow(10, place)) % 10;
}

function digitCount(num) {
  if (num === 0) return 1;
  return Math.floor(Math.log10(Math.abs(num))) + 1;
}

function mostDigits(nums) {
  let maxDigits = 0;
  for (let num of nums) {
    maxDigits = Math.max(maxDigits, digitCount(num));
  }
  return maxDigits;
}

function radixSort(arr) {
  const maxDigitCount = mostDigits(arr);

  for (let k = 0; k < maxDigitCount; k++) {
    // 创建桶
    const buckets = Array.from({ length: 10 }, () => []);

    // 将每个数字放入对应的桶
    for (let num of arr) {
      const digit = getDigit(num, k);
      buckets[digit].push(num);
    }

    // 将桶中的数字合并回原数组
    arr = [].concat(...buckets);
  }

  return arr;
}

// 示例用法
const array = [170, 45, 75, 90, 802, 24, 2, 66];
const sortedArray = radixSort(array);
console.log(sortedArray); // 输出：[2, 24, 45, 66, 75, 90, 170, 802]

睡眠排序

• 睡眠排序就是构造 n 个线程，让线程和排序的 n 个数对应。
• 例如对于[4,2,3,5,9]这样一组数字，就创建 5 个线程，每个线程睡眠 4s，2s，3s，5s，9s。这些线程睡醒之后，就把自己对应的数报出来即可。这样等所有线程都醒来，排序就结束了。
• 但睡眠排序由于多线程的问题，在真正实现上也有困难。

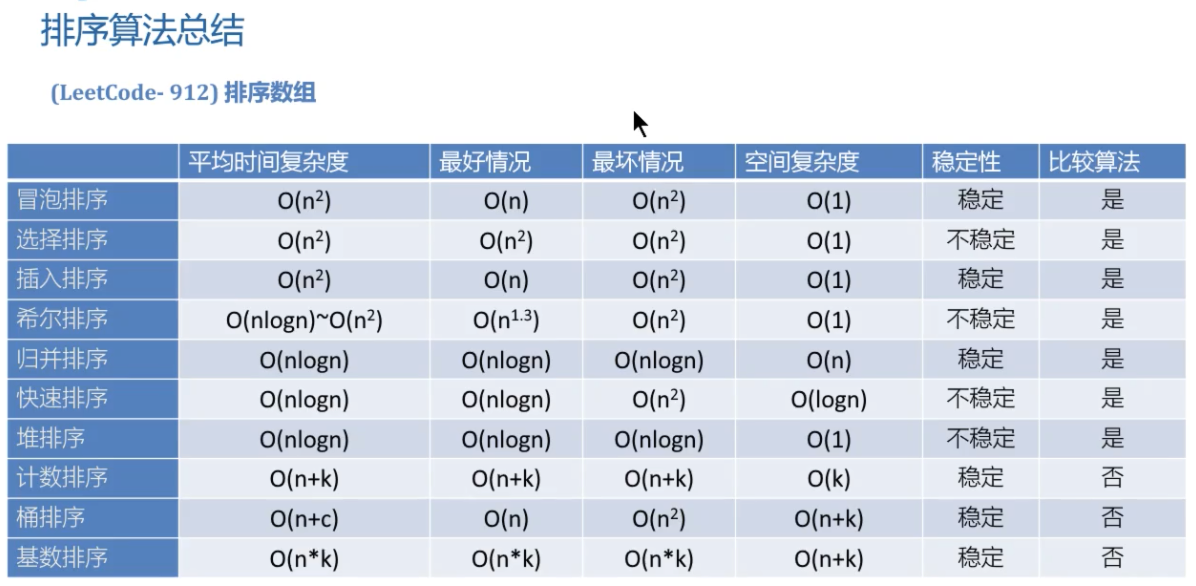
排序算法总结